
Therefore, the area of the shaded part of this figure would be 640.7 centimetres squared. So since eight is larger than five, it will round the six up to a seven. So we have to decide: do we keep the six a six or round it up to seven? So we look at the number to the right of it. But it says to round to the nearest tenth, so that’s one decimal place.
SHADED REGION CIRCLES IN RECTANGLE HOW TO
inscribed in a circle, How to Find the Area of a Rectangle within Another Rectangle. When we subtract, we find that the area of the shaded part is 640.68. How to find area of shaded region involving polygons and circles. And that equals 2339.24, and now we subtract. So let’s go ahead and take that number, multiply it by 𝜋, and then multiply it by two. So we get 2979.92 minus two times 𝜋 times 372.49.
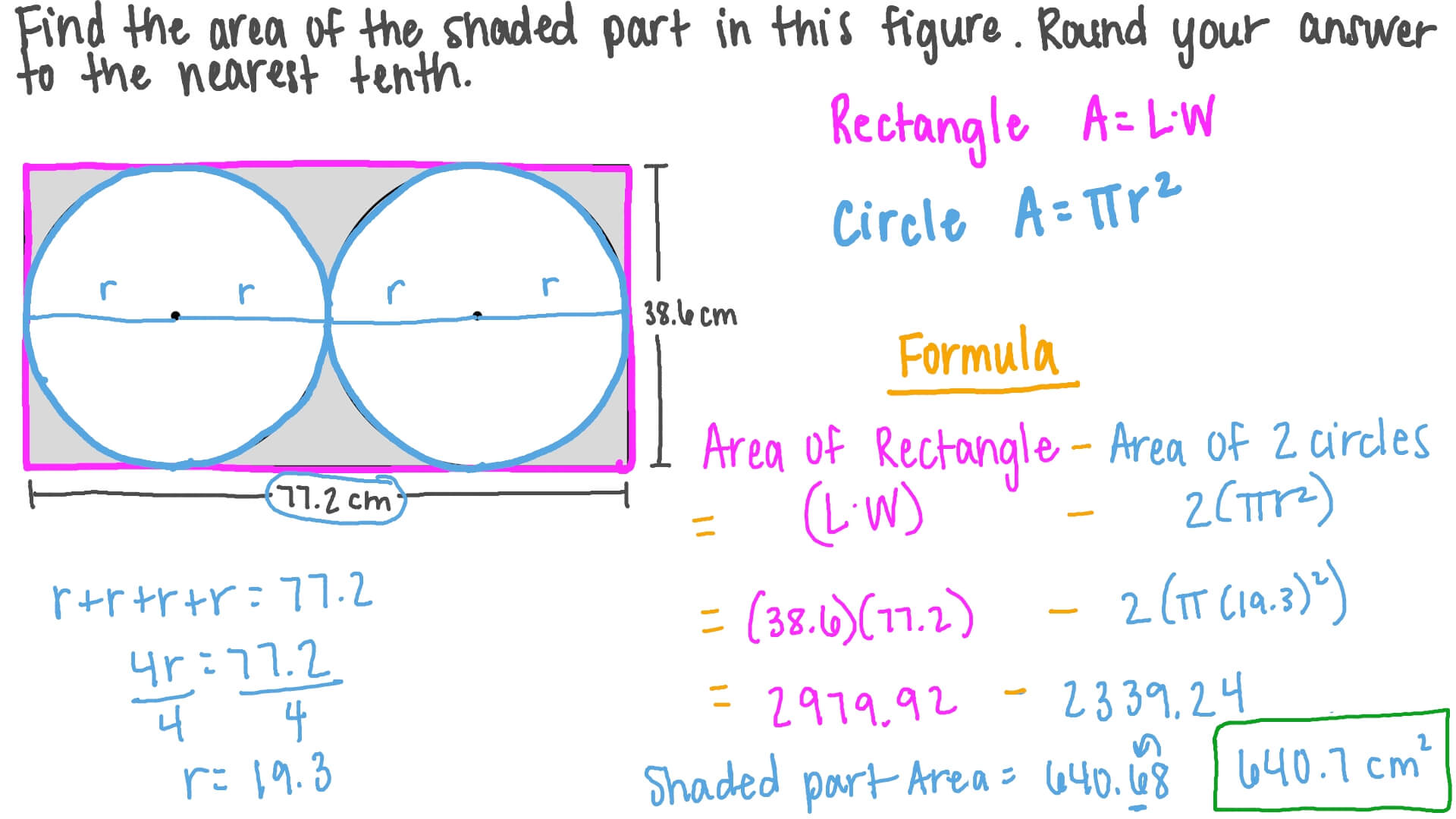
So we plug that in for 𝑟 and now we evaluate. And now we need to divide both sides by four.
SHADED REGION CIRCLES IN RECTANGLE PLUS
𝑟 plus 𝑟 plus 𝑟 plus 𝑟 would be four 𝑟. Can we make sense of the area bounded by a circle in the same way that we define the area of a rectangle Again it seems clear that the larger the radius of. So that means we could solve for the 𝑟, the radius. find the shaded area in the circle with a rectangle ( 3 x 4 ft dimension) inside the circle. So from here to here would also be a radius as well as this one as well as this one.Īnd notice all of these radii together should be equal to 77.2. And now we need the radii, which is the distance from the centre to an outside point on the circle. So the length and the width would be 38.6 times 77.2. I have been given two plots: (3,4) and (5,0).: Assuming that the circle center is at origin (0,0), look at a diagram it will be apparent that the radius 5: find the area of the circle A pi52 A 78. The shaded region is between the rectangle and the circle. It is enclosed by a circle with a radius of 10 meters. I need to find the area of a shaded region in which a rectangle is inside a circle. So we need to find the length, the width, and the radius of the circles. 20.47 Area of the circle r2 (3.14 × 6.5 × 6.5) cm 2 132.665 cm2 Area of the rectangle (12 × 5) cm 2 60 cm 2 Area of the shaded region. In the figure below is a rectangle with a length of 5 meters and a width of 4 meters. So the formula that we need to use would be the area of the rectangle minus the area of the two circles, which would be equal to length times width minus two times 𝜋𝑟 squared. So the shaded region is the entire rectangle, except for the circles, so we take those out. And there are also two circles and the area of a circle is equal to 𝜋 times the radius squared.

Here, we can see that we have a rectangle and its area will be length times width.

Find the area of the shaded part of this figure.


 0 kommentar(er)
0 kommentar(er)
